of the telescoping tube determines the
overall length accommodates the firing
effective area, and from this calculation
mechanism and mounting arrangement).
the diameter becomes 2.0 inches.
(2) Referring again to figure 20, it may be
d. Propellant Charge Weight.
determined that a catapult with a
separation velocity of 80 fps minimum
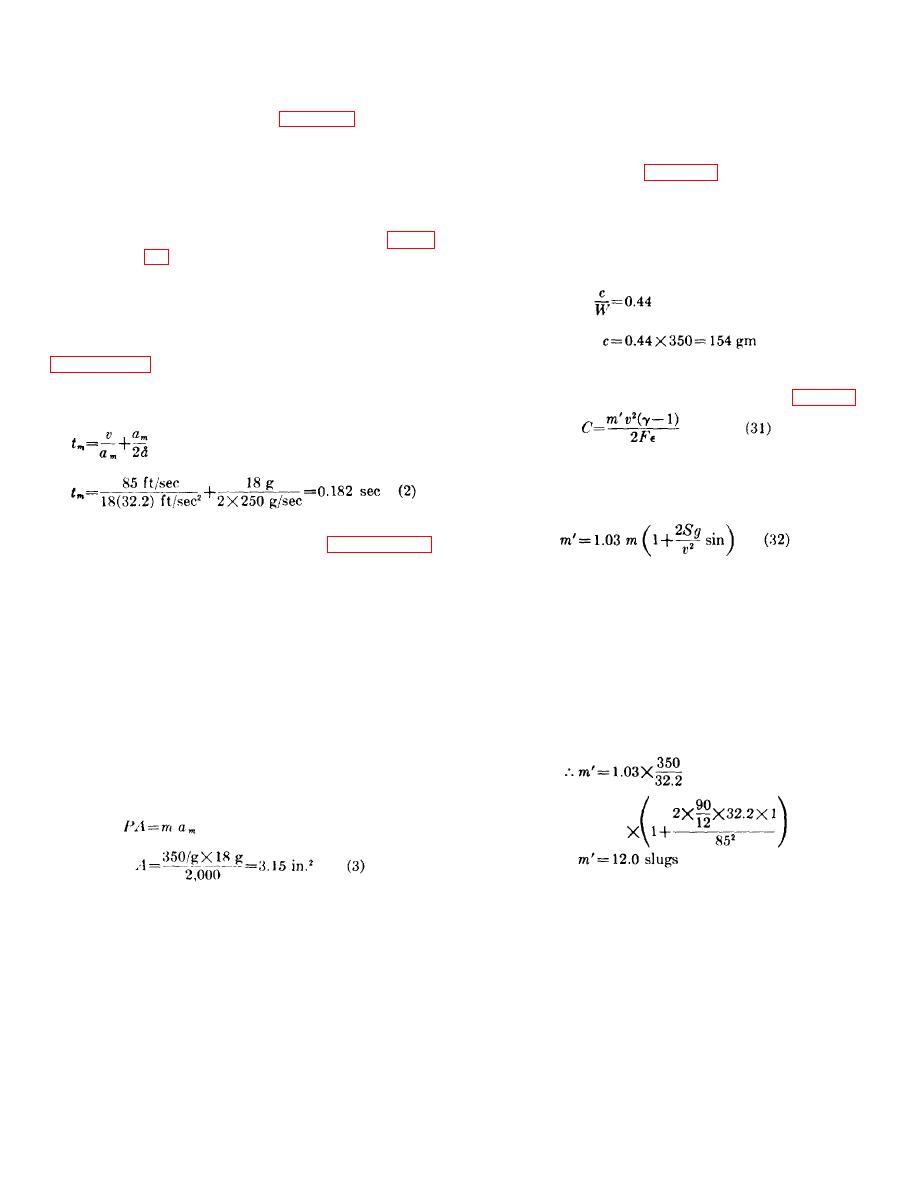
(1) The propellant charge weight is estimated
and an acceleration of 20 g maximum
by using figure 21. From this figure it
would require a stroke of 72 inches.
may be seen that the approximate ratio of
Since it is not practical to design to the
propellant charge to propelled weight for a
minimum velocity nor the maximum
catapult with a terminal velocity of 85 fps
acceleration, it is determined, using figure
is 0.44 gm/lb. Since the propelled weight,
W, is 350 pounds, the propellant charge,
be obtained with a stroke of 90 inches
c, is:
with an acceleration of 18 g. With these
approximate. values established. the
design is continued.
b. Stroke Time.
Using equation (2) from
(2) It is possible to refine this approximation
using equation (31) from the refinements
found in the previous approximation, and the rate of
to first order equations section (para. 51).
change of acceleration specified, the time is estimated
as follows:
(3) In this equation, m' is the modified
propelled mass, modified to correct for
friction effects and direction of ejection. It
may be calculated from equation (32):
c. Peak Pressure.
(1) To use equation (3) from paragraph 22,
either the peak pressure or the diameter
(4) The following values are assumed for use
of the catapult must be known. Since no
in equation (32):
diameters are specified in the design
m = propelled mass 350/g slugs
requirements, it is advantageous to
S = stroke to separation 90 in.
choose a peak pressure which experience
g = acceleration due to gravity
has shown will satisfy the design
32.2 ft/sec2
requirements without requiring unusually
v = velocity at separation 85 fps
large diameter tubes. The selection of the
a = angle between direction of
preliminary peak pressure is also
thrust and horizontal +
determined, in part., by the characteristics
90
(vertical-upward
of available propellants. Such a peak
ejection)
pressure is 2,000 psi. Using this figure in
equation (3), the effective area (a function
of diameter) of the catapult is found as
follows:
This corresponds very closely to a
(5) The charge weight may then be
diameter of 2 inches.
calculated using equation (31), assuming
(2) Peak pressure and acceleration occur
an
when the telescoping tube (intermediate
tube) and the inner tube are traveling
together. Therefore, the outside diameter
71


