Where:
r = linear burning rate
B = burning rate constant
P = maximum pressure
n = pressure exponent of burning rate
This form of the burning rate-pressure relationship will be found in other portions of this bulletin.
51. Refinements to First Order Approximations. a. Stroke Length.
(1) General.
(a) The problem considered will be to determine the minimum travel for a three-tube catapult when
given a required terminal velocity, v, and when limitations are set on the rate of change of
acceleration, , and on the maximum acceleration am.
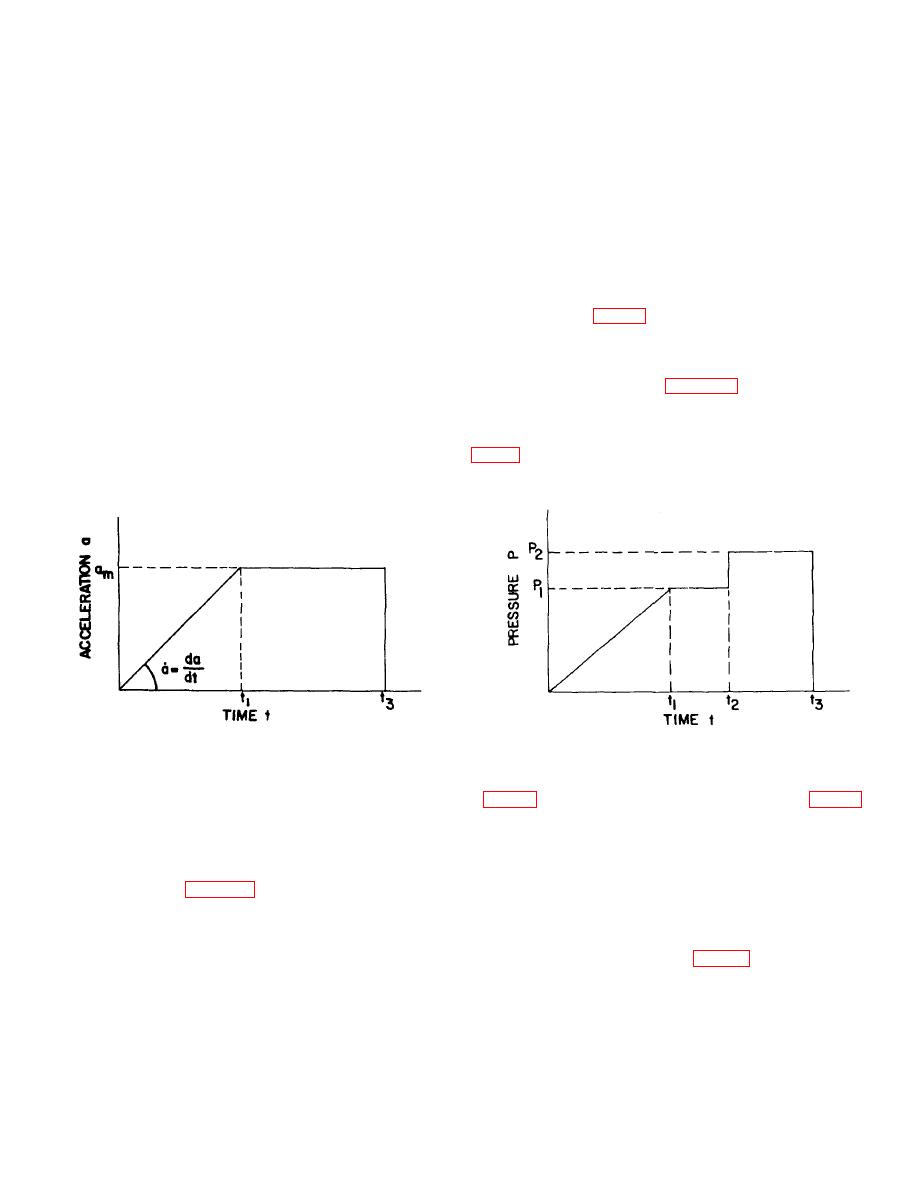
(b) The "ideal" acceleration-time curve for a catapult (shown in fig. 41) is constructed from the human
tolerance limits of acceleration, am,, and rate of change of acceleration, , in any specified ejection
direction. The physiological limitations are presented in Table 1, and in military specifications. The
initial slope of the acceleration-time curve is and the level portion is am. If a three-tube catapult is
assumed, the corresponding pressure-time curve would be as shown in figure 42. The point marked
t2, where an instantaneous rise in pressure is shown, corresponds to the initial movement of the inner
tube of the catapult when the telescoping tube stops. If the acceleration is to remain constant, the
applied force must also remain constant. Since the inner tube presents a smaller area to the gas
pressure than the telescoping tube (see fig. 2), the pressure must increase correspondingly to
provide a constant force.
Figure 41. "Ideal" acceleration vs time curve.
Figure 42. "Ideal" Pressure vs time curve.
(c) As it would be difficult, if not impossible, to attain it constant acceleration system, catapult designs
usually are based on a pressure time curve (fig. 43) from which all acceleration-time curve (fig. 44)
can be derived. The solid lines ill both figures show the desired operating conditions.
(d) Inasmuch as acceleration is proportional to the pressure acting on the catapult piston and the
velocity and travel are, at least ideally, tile first and second integrals of this acceleration, it is possible
to discuss the performance of a catapult in terms of its pressure characteristics. Curve 0-1-2 of
figure 45 illustrates the ideal pressure characteristics determined from limits of acceleration and rate
of change of acceleration currently used for human ejection in an upward direction. Conventional
catapults are designed to approach this ideal characteristic through the selection of interior ballistic
parameters and propellants. Catapults usually are designed so that the maximum design limitations
are met only at the high-temperature operating condition (curve A of fig. 45) performance is
appreciably lower when operating at 70F. and -65F. (curves
49


