T.O. 33B-1-1
3-11
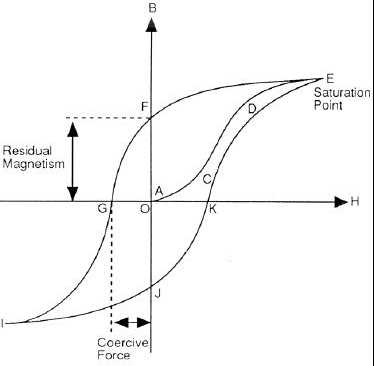
Figure 3-16. Hysteresis Curve for a Ferromagnetic Material
3.1.8.1
Hysteresis Curve.
The magnetic field within an unmagnetized piece of steel is zero. As the magnetizing force (H) is increased from zero,
the flux density (B) within the part will also increase from zero. The curve from points A to E in Figure 3-16 illustrates
this behavior. In the region of point E, the flux density increases up to a point and then tends to level off; this condition
is called magnetic saturation and for a magnetically saturated ferromagnetic material, the relative permeability (m) is
approximately equal to 1. When the magnetizing force is reduced to zero the flux density does not return to zero.
Instead, the flux density returns to a value shown at point F in Figure 3-16. This is the amount of residual magnetism
resulting from the applied magnetizing force (H) that reached the point E in the hysteresis curve. As the magnetizing
force (H) is increased from zero in the opposite direction, the flux density (B) will decrease to zero, as shown at point G
in Figure 3-16, and then start to increase to point I. The magnetizing force (H) represented by the distance OG on the
H axis in Figure 3-16 is called the coercive force. It represents the strength of the magnetizing force (H) required to
reduce the flux density (B) to zero in a saturated ferromagnetic material. A further increase in the magnetizing force
(H) to the point I results in saturation of the material in a direction opposite to that represented by point E. Reduction
of the magnetizing force (H) to zero from point I will reduce the flux density (B) to the value represented by point J.
Application of a magnetizing force (H) in the original direction will change the flux density (B) as shown in the portion
JK of the hysteresis curve. Increasing the magnetizing force (H) sufficiently will return the material to saturation as
illustrated at point E.
3.1.8.2
Magnetic Domains.
The behavior of ferromagnetic materials resulting in properties evidenced by hysteresis curves can be explained in
terms of magnetic domains. Domains are small regions within a ferromagnetic material that have a permanent
magnetic flux density (B) that is not equal to zero. In a completely demagnetized ferromagnetic material, the domains
are randomly oriented resulting in an overall flux density of zero. When saturated, the domains are all aligned in the
direction of the applied field. When the applied field is removed, after saturation, some domains return to their
previous orientation but most remain aligned in the direction of the previously applied field. This results in the
residual magnetism observed in ferromagnetic fields. The magnetic behavior then is a result of behavior of the
domains within the ferromagnetic material. Magnetization is the alignment of domains in a single direction;
demagnetization is a randomization of the alignment of the domains resulting in a zero net residual magnetism.