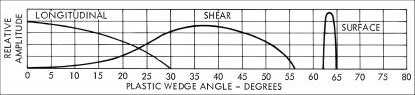
T.O. 33B-1-1 5-9 of the refracted beams are determined by Snell's law. Figure 5-11 shows the relative energy for shear, longitudinal, and surface  wave  beams  in  steel  for  different  incident  angles  of  longitudinal  waves  in  plastic.    The  curves  shown  were obtained  using  plastic  wedges  on  steel.    Similar  shaped  curves  can  be  obtained  for  other  test  materials,  such  as aluminum and titanium.  Similar curves can also be generated for the immersion mode of inspection with the plastic replaced by water.  Refraction angles are greater with water than plastic. a.     The incident angle at which the refracted angle for longitudinal waves reaches 90 degrees is called the first critical angle.  At incident angles equal to or greater than this critical angle, longitudinal waves no longer exist in the material.  Beyond this angle, only shear waves remain in the test material. Figure 5-11.  Relative Amplitude in Steel of Longitudinal, Shear and Surface Wave Modes with Changing Plastic Wedge Angle. b.     The incident angle at which the refracted angle for shear waves reaches 90 degrees is called the second critical angle.  At incident angles equal to or greater than this, shear waves are no longer generated in the material.  Instead, surface waves are propagated along the surface of the material. c.     Figure  5-11  shows  the  first  critical  angle  in  plastic  for  steel  is  approximately  30  degrees;  the  second critical angle is approximately 56 degrees. d.     Incident angles useful for shear-wave NDI fall between the two critical angles. 5.1.5.3 Obtaining the Required Refracted Beam. Field  NDI  personnel  are  responsible  for  using  the  correct  refracted  beam  angle  for  a  particular  application.    The specific  procedure  details  the  correct  refracted  beam  angle.    However,  it  is  important  for  the  field  NDI  inspector  to know how the correct angle was obtained.  Snell's law is the tool for determining wedge angles for contact testing, or the  angle  of  incidence  in  water  for  immersion  testing.    The  following  example  shows  how  Snell's  law  is  used  to determine the angle of incidence in plastic needed to generate 45-degree shear waves in aluminum: f2 = 45°; sin 45 = 0.707 v1 = velocity of longitudinal wave in plastic wedge = 1.05 x 105 in/sec (from Table 5-2) v₂ = velocity of shear waves in aluminum = 1.22 x 10⁵ in/sec (from Table 5-2) sin sin f f 1 2 1 2 ₌v v ; sin . . . f 1 5 5 0 707 1 05x10 1 22 10 = x or  sin (   . )(  . ) . . f1 5 5 0 707 1 05x10 1 22 10 0 608 = = x Therefore, f₁ = 37.5° (from Table 5-1) NOTE Then  determining  an  angle,  use  the  angle  having  the  sine  value  closest  to  the calculated  sine  value.    For  example,  if  sin  f₁  =  0.591,  Table  5-1  shows  sin  36  = 0.5878 and sin 37 = 0.5984.  Since 0.5878 is closer to 0.591, select 36.