(2) Equation of state.
PV = (Nn + k)RT
(41)
Where:
n = the number of moles of propellant gas per unit of propellant burned
N = weight of propellant burned
R = universal gas constant
T = space mean temperature
h. An analytical simultaneous solution of these equations is not possible because of the interrelationship of the
many dependent variables, and the fractional pressure exponent in the burning law, although they can be evaluated by
an analog computer. Attempts have been made to simplify their relationships by assuming that the heat loss is some
definite fraction of the kinetic energy of the moving mass, by modifying y (ratio of specific heats) to account for heat
losses, or by various other assumptions. Such simplifications are successful in describing the interior ballistics of guns
where the time cycle is much shorter and the heat losses are much smaller fractions (approximately 10 percent) of the
total energy produced by the propellant. The longer functioning time of a propellant actuated device (approximately four
or five times that of a gun) permits energy losses (mostly heat losses) of from 40 to 60 percent of the total available
energy and prevents the use of such simplifying assumptions without experimental measurement of energy losses.
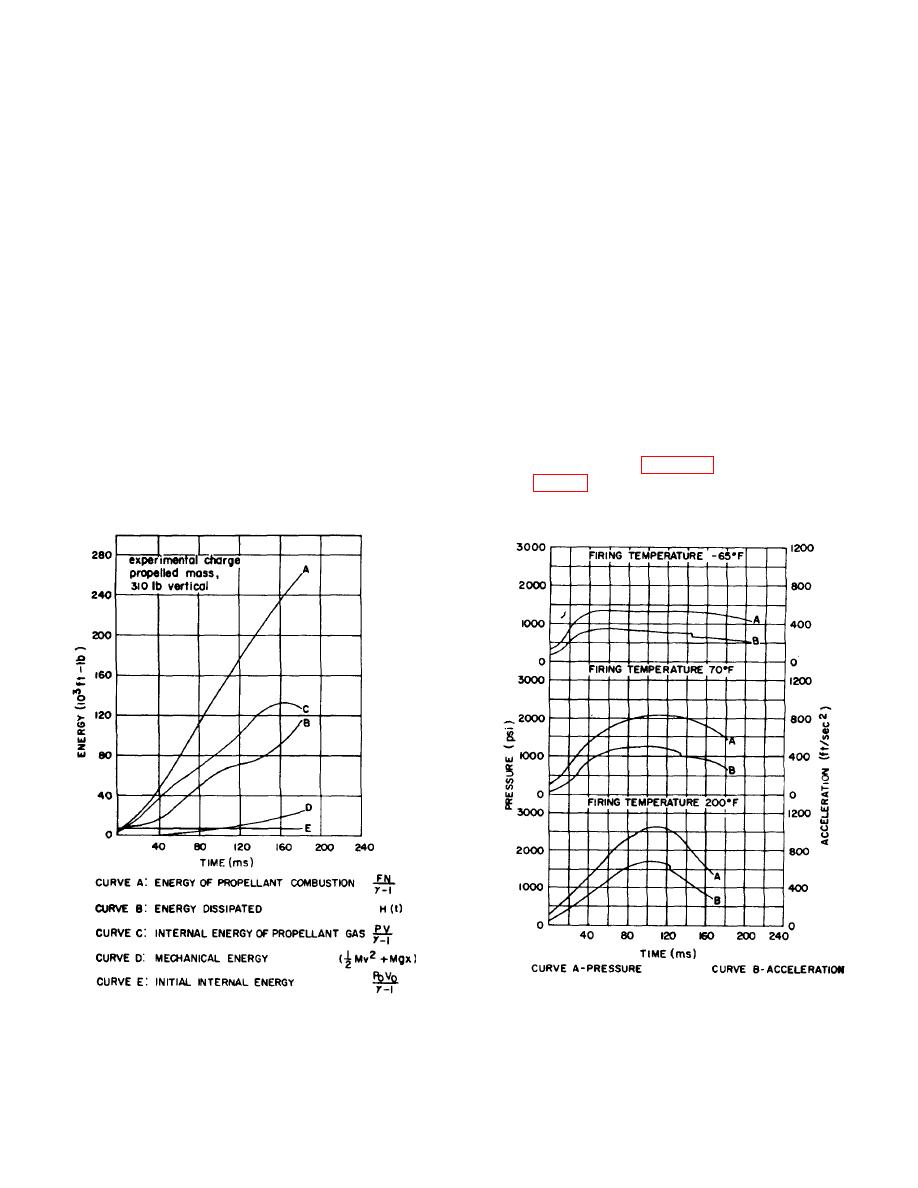
i. These usually are determined by analysis of pressure-time data. The results of figure 49 were obtained from a
computer analysis of the pressure-time and acceleration-time curves (fig. 50) for the M5 catapult. Use of analog or
digital computers makes detailed analyses of this type possible.
Figure 50. Pressure and acceleration vs time data
used in analysis of energy balance of M5 Catapult.
Figure 49. Energy balance of M5 Catapult (firing
temperature, 70F.)
64


