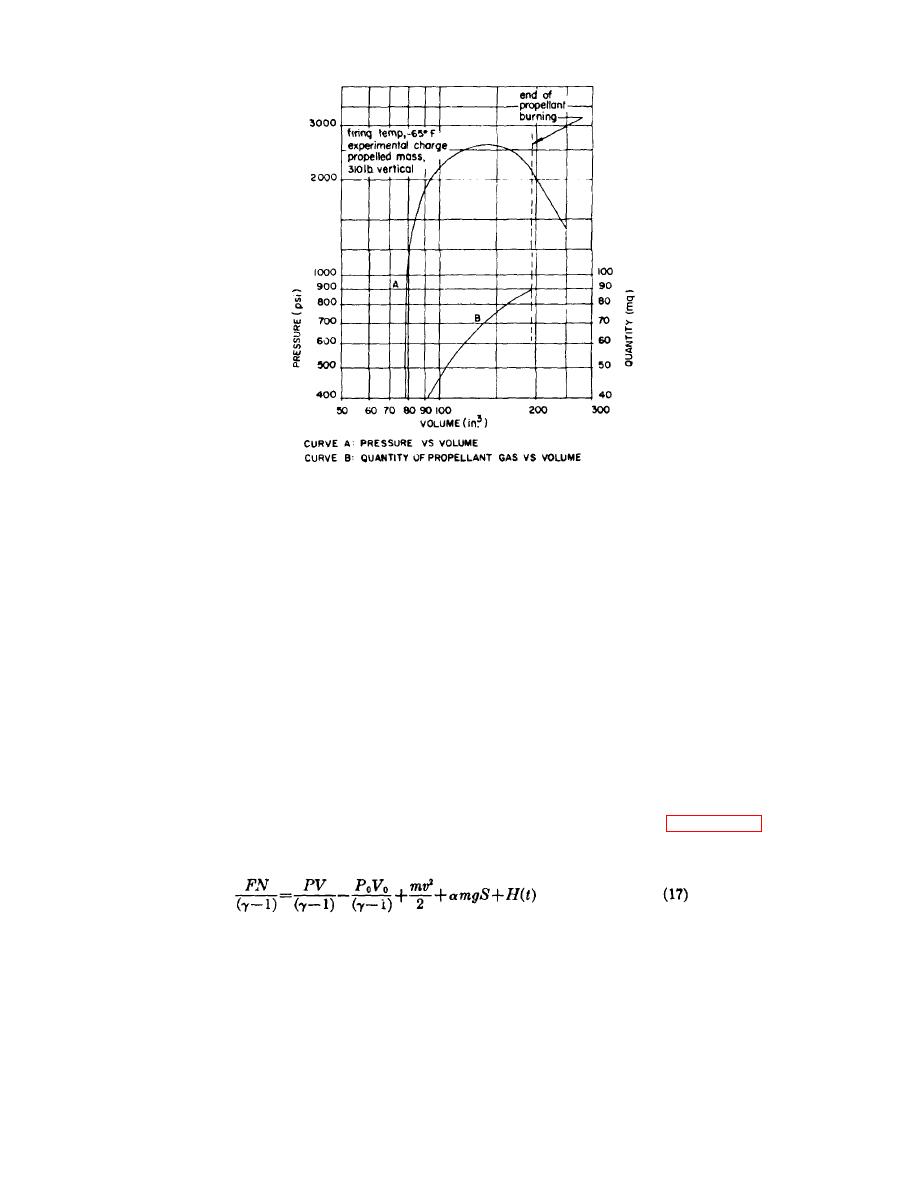
Figure 48. Pressure and quantity of propellant gas vs volume on logarithmic scales.
(3) The rate of recession, r, of each dimension of the propellant grain is dependent on the pressure, P,
n
according to the law: r=BP , where B and n are constants for a particular propellant composition and initial
temperature.
(4) Propellant gases are perfect gases with constant specific heats and molecular weights.
(5) The total energy made available by the combustion of the propellant is equal to the product of the mass of
propellant consumed and the specific energy of isochoric explosion (a constant dependent upon propellant
composition).
(6) Gas leakage is negligible.
(7) Work done against friction is negligible. (This assumption is applicable, in general, only to catapult
systems.) (8) The cartridge case ruptures when propellant combustion begins.
(9) Pressure, temperature, and composition of gases are assumed to be uniform throughout the chamber.
c. Although it is possible that none of these assumptions are completely valid in an actual ballistic system, they
simplify the problem of computation so greatly that they are used widely in interior ballistic calculations.
d. The assumptions discussed in b above, are embodied in the following equations which describe the interior
ballistic performance of catapults and removers, and, with slight modifications; thrusters. The modifications of these
equations to adapt them for an analysis of the interior ballistics of thrusters are discussed in paragraph 54.
(1) Conservation of energy.
Where:
F = impetus of propellant
N = gas produced
y = ratio of specific heats
61


