T.O. 33B-1-1
6-38
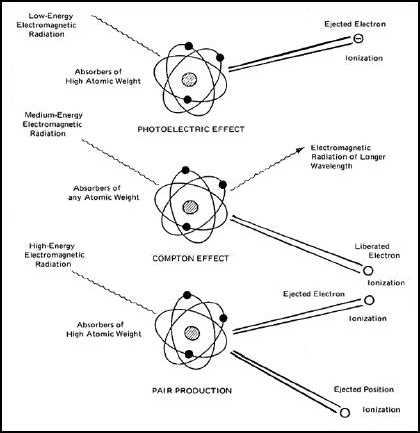
Figure 6-15. Illustration of Various Radiation Absorption Interactions.
6.5.1.1
Photoelectric Absorption.
When the photons have energies of 100 keV or less, they are readily absorbed by the electrons in the orbital shells of
the atoms of the absorber. The energy of the photon is transferred to the electron; often dislodging it from its orbit and
the remainder of the energy in the photon is used to give the electron kinetic energy or velocity. These ejected electrons
are called photoelectrons and the process is known as photoelectric absorption. The moving electrons then lose their
energy, producing ion pairs. It should be noted that the radiation photon has given up all of its energy and no longer
exists. This mechanism of absorption has a very high probability for very low energy radiation and accounts for the
major absorption of radiation when photon energies are 100 keV and less.
6.5.1.2
Compton Effect.
When the photon energies are in the 100 keV to 10 MeV range, all of the energy is not required to dislodge an orbital
electron and accelerate it by induction of kinetic energy. In this case the photoabsorption can occur, but the photon
continues at some different path and at a reduced energy level, due to the loss of energy to the electron. By this
mechanism of absorption, the path of the photon is altered and its energy decreased. This mechanism of absorption is
referred to as Compton effect. Compton effect accounts for the major absorption of radiation in the energy range
between 100 keV and 10 MeV.
6.5.1.3
Pair Production.
When photon energies exceed 1.02 MeV, their energy can cause pair production. In this event the high-energy photon
is disintegrated by the nuclear field surrounding the nucleus of the atom. The energy of the photon converts into an
electron-positron pair. The positron has the same mass as an electron and is of equal, but opposite charge. It may be
noted that in this absorption mode, the energy of the massless photon is converted to mass. Einstein's equation states
that energy equals mass times the square of the velocity of light (E = mc2). If this equation is used it can be found that