T.O. 33B-1-1
3-40
Example:
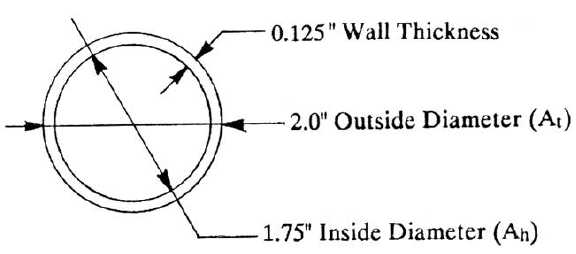
What would the effective diameter be for a cylindrical part 10 inches long that has a 2 inch
outside diameter with a 0.125 inch wall thickness (see Figure 3-26).
Figure 3-26. Calculating Effective Diameter
To find At, calculate the cross-sectional area of the outside diameter of the part as follows:
At = pr2
At = p(1)2
At = 3.1416 sq. inches
To find Ah, calculate the cross-sectional area for the inside diameter of the part (the part’s hollow portion)
as follows:
Ah = pr2
Ah = p(0.875)2
Ah = 2.40 sq. inches
Insert the results for At and Ah into the formula to find Deff.
Deff
=
-
231416
2
3
1416
1
2
.
.40
.
Deff = 0.97 inch
To calculate the current required to longitudinally magnetize the part in the above example, use the formula
from paragraph 3.3.12.6.3.1 (for the part in the bottom of a 12 inch diameter coil with 5 turns),
except replace D with Deff. (0.97):
I
KD
NL
=
I
=
45000
0
97
5
10
.
I = 873 amperes